
Tant que l'on s'en tient aux rectangles et aux triangles, la notion d'aire est élémentaire. En les décomposant en triangles, on peut également facilement définir l'aire des polygones, ce qui permet a priori d'approcher celle de tous les domaines du plan. En fait, non ! C'est plus compliqué que cela : on doit distinguer entre les domaines, que l'on dit quarrables, possédant une aire, et les autres (voir le Calcul intégral, Bibliothèque Tangente 50). Mais ici, nous nous restreindrons aux domaines quarrables. La propriété essentielle est alors la suivante : l'aire est additive. Plus précisément, si l'on considère deux domaines dont l'intersection est d'aire nulle (c'est le cas des lignes), alors l'aire de leur réunion est égale à la somme des aires.
Sous la courbe, la surface
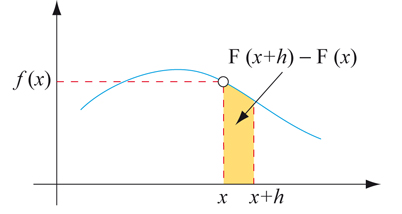
Admettons que, si f est continue (et positive) sur un intervalle I, le domaine situé sous la courbe d'équation y = f(x) entre les abscisses a et x possède une aire, que l'on note F(x). La propriété d'additivité permet alors d'affirmer que l'aire sous la courbe entre les abscisses x et x + h vaut F(x + h) – F(x). Si h est petit, on peut l'approximer par un rectangle de largeur h et de hauteur f(x), soit
F(x + h) – F(x) ≈ h f (x).
On ... Lire la suite
