On peut jouer avec les aires pour calculer π, mais on peut aussi partir de π pour choisir des aires. Pour changer, plutôt que la célèbre méthode d'exhaustion d'Archimède, on peut remettre au goût du jour une approche historique sans doute due aux Égyptiens... Ferez-vous mieux ?

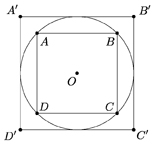
L'aire S d'un disque de rayon r est donnée par la fameuse formule . Calculer l'aire du disque unité (r = 1), c'est donc déterminer la valeur de . C'est ainsi que toute approximation du disque unité par une forme géométrique dont on sait calculer explicitement l'aire fournit une évaluation de , d'autant plus précise que la forme en question est « proche » du disque. Avec des carrés, par exemple, on peut faire comme ci-dessous.

L'aire de ABCD est donc plus petite que , tandis que celle de A'B'C'D' est plus grande que . Puisque A'B' est égal à 2 (c'est le diamètre du cercle), l'aire de A'B'C'D' est égale à 4, et donc < 4. D'autre part, la diagonale [AC] du carré ABCD est un diamètre du cercle, donc AC = 2. Dans un carré, le rapport diagonale/côté vaut  , le côté de ABCD est donc de  , c'est-à-dire . On en déduit que l'aire de ABCD vaut . Finalement donc, on a les inégalités .

On a vu ... Lire la suite