
Ne vous laissez pas impressionner par le vocabulaire : un corps n'est rien d'autre qu'un ensemble où il est possible d'effectuer des additions, des soustractions, des multiplications et des divisions selon les règles habituelles.
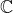 , complet au sens analytique, inachevé au sens algébrique
, complet au sens analytique, inachevé au sens algébrique
Attardons-nous d'abord sur l'ensemble , celui des nombres rationnels (quotients de deux entiers), car il correspond à un certain achèvement, que n'ont ni
, ni
, respectivement ensembles des entiers positifs et relatifs. Les quatre opérations y ont bien leurs propriétés habituelles (associativité, commutativité, distributivité), mais, de plus, leurs résultats restent dans
. Autrement dit, elles y sont « internes » à l'exception près que l'on ne peut pas diviser par zéro. En résumé,
est un corps et, dans ce sens, il a un côté « achevé ».
Le corps convient pour toutes les applications pratiques où les approximations suffisent. Cependant, il ne contient aucun nombre correspondant à certaines quantités géométriques simples, comme la longueur de la diagonale d'un carré de côté unité. Celle-ci peut seulement être approchée. On peut obtenir une suite d'approximations qui approchent ... Lire la suite
