Le développement du binôme

On a coutume de nommer l'expression (1 + x)ⁿ binôme de Newton, même si elle était utilisée bien avant la naissance de Newton, en particulier par les mathématiciens perses dès le x^e siècle, de même que le « triangle de Pascal » qui lui est associé. La formule du binôme concerne le développement de (1 + x)ⁿ comme somme de multiples des polynômes 1, x, x², x³, etc.

Pour n = 2 et n = 3, on trouve les identités remarquables (1 + x)² = 1 + 2x + x² et (1 + x)³ = 1 + 3x + 3x² + x³.

On passe à la puissance 4 en remarquant que (1 + x)⁴ = (1 + x)(1 + 3x + 3x² + x³).

En généralisant ceci, on obtient le tableau ci-dessous, où les développements des binômes de la colonne de gauche se lisent sur la ligne correspondante. Ainsi en quatrième ligne, on lit (1 + x)⁴ = 1 + 4x + 6x² + 4x³ + x⁴.

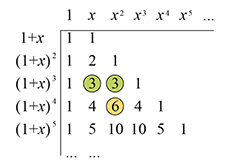Triangle ... Lire la suite gratuitement