
En mathématiques, le terme « identité » a un sens bien précis. Il s'agit d'une égalité vraie quelles que soient les valeurs de ses arguments, s'il y en a. Ainsi, cos2 x + sin2 x = 1 en est une. Dans l'enseignement secondaire, les identités remarquables concernent surtout des expressions du second degré. Dans l'enseignement supérieur, on rencontre quelques égalités concernant des polynômes de bas degrés, comme (a + b)(a2 – ab + b2) = a3 – b3. Dans les autres cas, on parle généralement de formules, comme pour celle du binôme ou les fameuses formules de trigonométrie. La question est plus de nature linguistique que mathématique…
Trois classiques en image
Comment calculer l'aire du grand carré de l'image ci-dessous ? Soit en considérant que son côté est de longueur a + b, ce qui donne une aire de (a + b)2, soit en additionnant les aires de chacun des quatre morceaux qui le constituent, ce qui donne a2 + 2ab + b2.
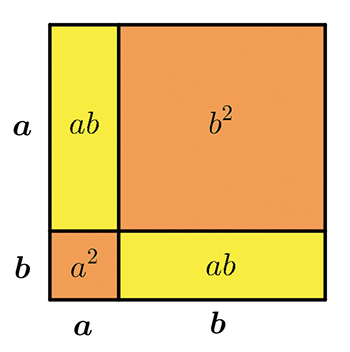
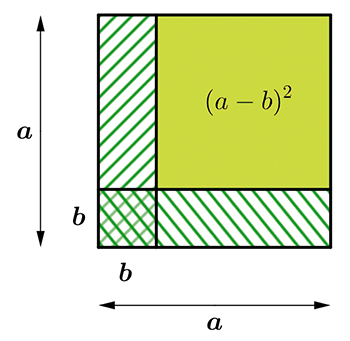
La même figure vue autrement permet d'établir que (a – b)2 = a2 – 2ab + b2. En effet, l'aire du carré vert, de côté a – b, peut aussi être obtenue à partir de celle du grand carré de côté a. Il suffit de retrancher l'aire des deux grands rectangles hachurés d'aire ab. L'aire du petit carré de côté b hachuré deux fois a alors été retirée une fois de trop. On rétablit cela facilement en écrivant que l'aire du carré vert est finalement égale à a2 – 2ab + b2.
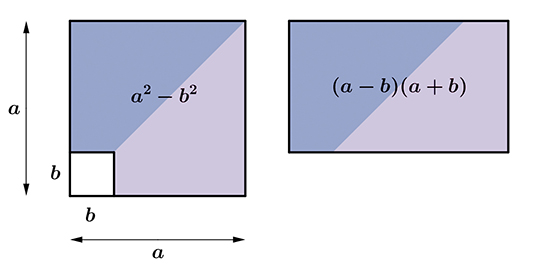
La troisième identité remarquable classique s'obtient aussi par découpage. Ici, le dessin parle de lui-même, il suffit de réassembler deux trapèzes pour former un rectangle.
Dans l'espace aussi !
Les découpages effectués dans le plan peuvent aussi se réaliser dans l'espace. On peut par exemple recouvrir un cube de côté a de quelques pavés bien choisis pour obtenir un cube de côte a + b. On obtient alors le développement de (a + b)3.

a3. a3 + 3a2b. a3 + 3a2b a3 + 3a2b + 3ab2 + b3
+ 3ab2. = (a + b)3
