Les échelles semi logarithmiques
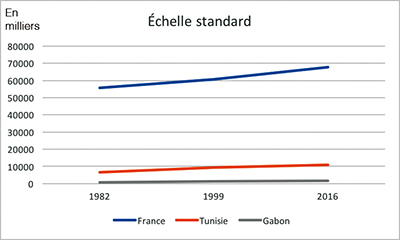
Supposons que l'on s'intéresse à la variation de la population de différents pays. Parmi eux, la France et le Gabon ont les tailles qui diffèrent énormément. Mettons en abscisse les années de recensement et en ordonnées la population. Dans un repère habituel, la courbe décrivant la population du Gabon sera écrasée sur l'axe des abscisses, et les variations seront imperceptibles.
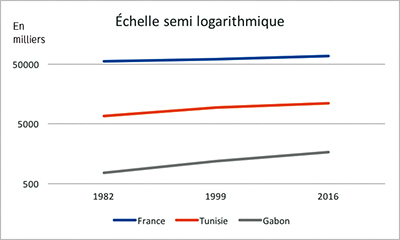
Pour permettre une lecture claire des données, on gradue l'axe des ordonnées suivant une échelle logarithmique ; ainsi, l'écart entre cent mille et un million est le même qu'entre un million et dix millions. Dès lors, la pente des segments de droite de chaque courbe représente l'accroissement relatif, et non absolu.
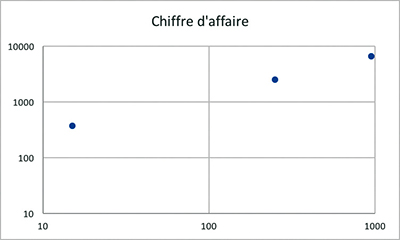
On peut également graduer les deux axes en échelles semi logarithmique. Ceci est intéressant si l'on veut représenter le chiffre d'affaire de plusieurs entreprises de tailles très différentes en fonction du nombre de leurs salariés : cela permet de rendre visible la position des plus petites d'entre elles. Les droites parallèles à la première bissectrice correspondent aux entreprises de même productivité par employé, alors que pour une graduation habituelle, ce sont les droites passant par l'origine.