Les Babyloniens déjà, entre 1800 et 1600 avant notre ère, savaient calculer la longueur de la diagonale du carré connaissant son côté ; les mathématiciens indiens du VIe siècle avant notre ère aussi. Le vrai problème de la nature de ce rapport entre diagonale et côté, c’est-à-dire pour nous s’est posé aux géomètres grecs : est-ce un rationnel, c’est-à-dire un quotient de deux entiers ?
√2, le rebelle !
Ce sont vraisemblablement les pythagoriciens, pour qui « tout est nombre », qui ont prouvé que le nombre en question était réfractaire à toute mise sous forme de fraction : ce nombre est bien irrationnel.
On doit la révélation de cette découverte, 530 avant notre ère, au disciple de Pythagore Hippase de Métaponte qui « le premier fit sortir du mystère la considération de l’irrationnel », d’après le philosophe Proclus (412‒485).
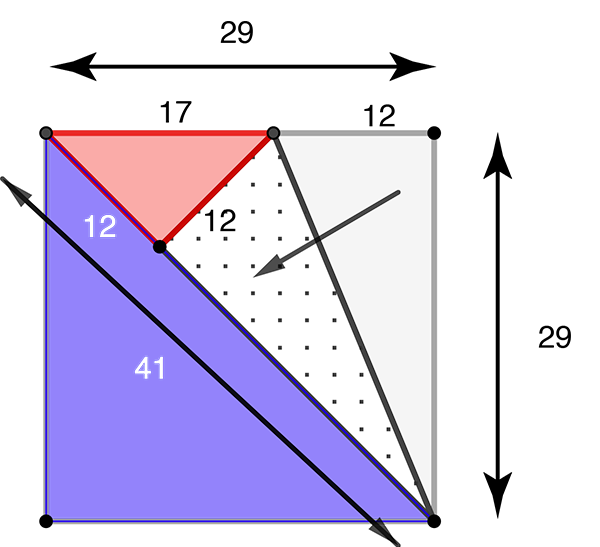
Si on a pu, comme Aristote, démontrer par l’absurde que n’est pas rationnel, les pythagoriciens ont, eux, privilégié pour ce faire les arguments géométriques, retranchant par exemple le côté du carré à sa diagonale. En effet, si la diagonale d’un carré de côté 29 était égale à 41, autrement dit si
était égal à
alors, les triangles colorés ayant même forme, on aurait aussi
Quelle contradiction !
Les contradictions de √2.
Un nombre utilisé… sans le savoir
Quand on parle du nombre beaucoup se disent : « Ah ça, c’est pour les matheux… Moi, ça ne m’intéresse pas, je n’ai jamais vu ce nombre. » S’ils savaient !
Eh oui, quiconque a manipulé des feuilles de papier, par exemple en format A4, a rencontré car ce nombre est le rapport entre les deux dimensions de la feuille : 297 mm sur 210 mm.
Le rapport vaut alors qu’une valeur approchée de
est 1,414213… Alors, oui, il y a un écart à la quatrième décimale, qui est dû au fait que, dans la pratique, les dimensions sont arrondies. Avec une largeur de 210 mm, il faudrait que l’autre dimension soit égale à 296,98 mm pour avoir un rapport qui « se rapproche davantage » de
!
Ce format de papier A est défini par une norme et vérifie une propriété remarquable : une feuille qui est coupée dans le sens de la largeur en deux parties égales produit deux feuilles semblables à l’original, c’est-à-dire avec le même rapport longueur/largeur. Comme l’aire est divisée par 2, cela veut dire que le rapport vaut
. Et, bien sûr, cela est vrai que la feuille soit au format A2, A3, A4 ou A5.
Divine (?) proportion
N’est-ce pas aussi Hippase de Métaponte qui a su, le premier, inscrire dans une sphère un dodécaèdre régulier, dont toutes les faces sont des pentagones réguliers ? Il a alors été confronté, comme pour au rapport de la diagonale au côté d’un tel pentagone : c’est devenu le célèbre nombre d’or, de valeur exacte
et dont une valeur approchée vaut 1,618. À la rationalité tout aussi défaillante que
on peut l’obtenir par le même genre de pliage que celui du carré.
Certains historiens pensent que c’est le nombre d’or, et non , qui a été le premier nombre irrationnel reconnu comme tel. Le débat fait encore rage !
On a désigné le nombre d’or avec la lettre grecque φ, sans doute en hommage au sculpteur du Parthénon, Phidias. De par sa définition, φ est la plus grande des solutions de l’équation x2 ‒ x ‒ 1 = 0, ce qui permet de dire qu’il est algébrique. Euclide, quant à lui, le définissait par le « partage en moyenne et extrême raison », c’est-à-dire le partage d’un segment en deux parties de longueur a (la plus grande) et b, telles que
On a alors
Selon les mots d’Euclide, « une droite est coupée en moyenne et extrême raison quand, comme elle est toute entière relativement au plus grand segment, ainsi est le plus grand par rapport au plus petit ». Les Anciens attribuaient déjà à ce nombre des propriétés mystiques, et Luca Pacioli (vers 1445‒1517) l’a même appelé « divine proportion ». « Divine », peut-être, mais irrationnelle !
Comment les écrire ?
Ces deux nombres, et φ, ont, bien sûr, des développements décimaux. Comme ils sont irrationnels, ces derniers ne sont pas périodiques.
On a : = 1,414 213 562 373 095 048 801… et φ = 1,618 033 988 749 894 848 204…
Rien de remarquable !
Par contre, leurs développements en fraction continue, eux, le sont :
(Raphaël Bombelli, 1572),
car
et
car
C’est vrai, qu’en tant qu’irrationnels quadratiques, c’est-à-dire racine chacun d’un polynôme de degré 2, leurs développements en fraction continue sont périodiques ; mais là, dans les deux cas, la période est très simple !
De plus, le nombre d’or admet un développement « en racine continue » (sous la forme de radicaux imbriqués), lui aussi élémentaire :
car
Le mythe du nombre d’or
Lorsqu’on évoque le nombre d’or, ses supposées vertus esthétiques viennent immédiatement à l’esprit. Comment un simple nombre, ayant certes beaucoup de propriétés, peut-il jouir d’une telle place dans l’imaginaire collectif ?
Ce mythe d’un nombre évoquant des proportions esthétiques idéales a été véhiculé par de nombreux écrits. Si Luca Pacioli le met en évidence dans son ouvrage De Divina Proportione, ce sont ensuite des auteurs comme Adolf Zeising (1810‒1876) et surtout Matila Ghyka (1881‒1965) qui ont donné du crédit à la thèse d’un attrait pour la « section dorée ». Des recherches pseudo-scientifiques, comme celles du philosophe et psychologue Gustav Theodor Fechner (1801‒1887), ont aidé à propager cette théorie.
Entraînés par cette aura supposée du nombre d’or, des critiques d’art et des artistes se sont engouffrés dans cette traque mystique. Des œuvres sont analysées, découpées, des tracés imaginaires sont suggérés à la surface des toiles et des bâtiments, et lorsque des rapports de longueurs « proches » de la valeur 1,618 émergent, alors des conclusions hâtives sont formulées et le lien entre l’esthétique d’un tableau et la présence de φ est supposé établi.
Il est indéniable que les artistes ont souvent recherché des règles permettant de s’approcher d’une esthétique « la plus parfaite possible », que ce soit avec la perspective, les harmonies de couleurs ou enfin le recours à des proportions. Il ne semble pas que le nombre d’or ait été plus présent que des rapports élémentaires. Des proportions comme 1/4, 3/8, 1/2, 5/8, 3/4, ou encore la règle des tiers chez les photographes, sont souvent jugées idéales.
Quelques artistes ont voué au nombre d’or une admiration sans faille et ont cherché à l’intégrer dans leur travail. Parmi eux, on retrouve les peintres Paul Sérusier, Maurice Denis ou les artistes du Groupe de Puteaux, appelé aussi Section d’or. Ils ont prôné une peinture idéale régie par des lois très strictes et le recours au nombre d’or, symbole mystique et divin. En réalité, ils l’utiliseront peu dans leurs compositions, peut-être à cause de la difficulté à le mettre en œuvre, contrairement aux divisions simples, plus faciles à utiliser.
Il est intéressant de voir comment ce nombre φ a pu acquérir une telle aura dans le monde artistique et dans l’imaginaire collectif. Et même s’il s’avérait réellement présent dans quelques œuvres, combien d’autres, communément réputées très esthétiques, ne le recèlent pas dans leur construction !
références
•
Le fabuleux destin
de √2. Benoît Rittaud,
Le Pommier, 2015.
•
Les équations
algébriques.
Bibliothèque
Tangente 22, 2005.
•
Dossier « La vérité
sur le nombre d’or ».
Tangente 203, 2022.