
La même formule est présente sur un timbre-poste de Suisse, émis le 6 mars 2007 pour célébrer le tricentenaire de la naissance de Leonhard Euler, et sur un timbre d’Allemagne de l’Est, émis le 6 septembre 1983 pour commémorer le bicentenaire de son décès.

La formule d’Euler énonce que e ‒ k + f = 2 (que l’on écrit plutôt, en français, s ‒ a + f = 2), c’est-à-dire que, dans l’espace, le nombre s de sommets moins le nombre a d’arêtes plus le nombre f de faces d’un polyèdre convexe est invariablement égal à 2.
Tout n’est pas en dimension 3
La formule d’Euler est-elle généralisable ? Observons les dimensions inférieures à 3, en utilisant la notation ai pour désigner le nombre d’éléments de dimension i présents dans l’objet de dimension n. Pour le point, a0 = 1 : on a simplement un point.
Pour le segment, a0 ‒ a1 = 1 : on est en présence de deux points et d’un segment
(et 2 – 1 = 1).
Pour un polygone, a0 ‒ a1 + a2 = 1 : on a affaire à n points, n segments et une surface
(et n ‒ n + 1 = 1).
Pour un polyèdre, a0 ‒ a1 + a2 ‒ a3 = 1 : on retrouve la formule d’Euler pour un volume (avec a0 = s, a1 = a, a2 = f et a3 = 1).
La formule d’Euler pour les polyèdres réguliers
Prenons un polyèdre régulier dont les faces sont m triangles équilatéraux. Le nombre de sommets est noté s.
On a donc, d’après la formule d’Euler :
Il est d’ailleurs possible d’utiliser le théorème du déficit d’angle, à savoir ici (en degrés) la relation
pour obtenir le même résultat, à savoir 2s = m + 4.
D’autre part, le nombre k d’angles à un sommet, soit est égal à 3, 4 ou 5 (car k > 2 et k × 60° < 360°).
Il y a donc trois polyèdres réguliers dont les faces sont des triangles :
le tétraèdre (pour lequel s = 4 et m = 4), l’octaèdre (avec s = 6 et m = 8) et l’icosaèdre (où s = 12 et m = 20).
Si le polyèdre régulier a m faces carrées, on a, de la même façon :
Idem par le théorème du déficit d’angle :
soit 2s = 2m + 4.
D’autre part, le nombre k d’angles à un sommet, égal à ne peut être égal qu’à 3. Il n’y a donc qu’un seul polyèdre régulier dont les faces sont des carrés : le cube (pour lequel s = 8 et m = 6). Si enfin le polyèdre régulier possède m faces pentagonales, on a
. Par le théorème du déficit d'angle, on obtient
, soit 2s = 3m + 4.
D’autre part, le nombre k d’angles à un sommet, qui vaut ne peut être égal qu’à 3. Il y a donc qu’un seul polyèdre régulier dont les faces sont des pentagones : le dodécaèdre (pour lequel s = 20 et m = 12).
Au final, il n’existe que cinq polyèdres convexes réguliers :
le tétraèdre, qui est son propre dual, le cube et son dual, l’octaèdre, l’icosaèdre et son dual, le dodécaèdre.
Références
• Dossier « La saga des théorèmes : la formule d’Euler ». Tangente 174, 2017.
• Leonhard Euler. Bibliothèque Tangente 29, 2007.
• Relation d’Euler et les polyèdres sans « trou ». Cellule de géométrie
du Centre de recherche de la Haute École de la Communauté française en Hainaut, 2023, disponible en ligne.
Le mathématicien français Henri Poincaré (1854‒1912) a démontré que, pour un polytope convexe de dimension n quelconque, on a bien : a0 ‒ a1 + a2 ‒ a3 +… + (‒1)nan = 1, ce qui s’écrit de manière plus concise avec en fait an = 1 (le polytope étant supposé convexe, il est également connexe).
La convexité (propriété géométrique selon laquelle chaque fois que l’on prend deux points dans le polytope le segment qui les relie est lui aussi tout entier dans le polytope) est une condition suffisante, mais non nécessaire pour que la formule d’Euler s’applique au polytope. Par contre, cette dernière ne s’applique plus pour des formes plus sophistiquées, par exemple « avec des trous ».

Le tesseract.
Pour un « volume » en dimension 4 (ou polychore), comment concrétiser l’expression
a0 ‒ a1 + a2 ‒ a3 + a4 = 1 ?
L’hypercube en quatre dimensions, nommé tesseract, peut être représenté dans un plan (en deux dimensions) sous la forme d’une vue en perspective tridimensionnelle, comme le montre le schéma. Cette représentation (il en existe d’autres) facilite le comptage des cubes tridimensionnels présents dans le tesseract.
L’origine O du repère orthonormé (O, x, y, z, w) dans lequel le tesseract est représenté se trouve au centre de la figure ; l’axe (Ow) n’est pas visualisable. La coordonnée w est proportionnelle au côté du cube sur la figure ; ainsi le « petit » cube de la figure est-il plus proche de O que le « grand ».
Un carré standard en deux dimensions peut être dupliqué dans une troisième dimension pour former un cube, les deux carrés étant reliés par quatre arêtes et quatre faces supplémentaires. De la même façon, un cube peut être dupliqué dans la quatrième dimension pour former un tesseract, les deux cubes étant reliés par huit arêtes, douze faces et six cubes supplémentaires.
Parmi les huit cubes, on trouve les deux cubes issus de la duplication, tous les deux étant décrits dans le repère (O, x, y, z), positionnés respectivement en w1 et en w2. On y trouve aussi les six interstices compris entre les faces de ces deux cubes : deux sont décrits dans (O, w, x, y) à deux coordonnées z1 et z2 ; deux autres sont décrits, de la même manière, dans le repère (O, w, x, z) et les deux derniers dans le repère ( O , w , y , z ) .
Petit voyage dans la 4D
Construisons le tesseract en deux étapes. Au cube (pour lequel a0 ‒ a1 + a2 ‒ a3 = 8 – 12 + 6 – 1 = 1), ajoutons un point dans la quatrième dimension pour former une hyperpyramide (ou un hypercône).
L’expression devient alors :
(a0 + 1) ‒ (a1 + 8) + (a2 + 12) ‒ (a3 + 6) + 1 = (8 + 1) – (12 + 8) + (6 + 12) – (1 + 6) + 1 = 1.
À partir de là (a0 ‒ a1 + a2 ‒ a3 + a4 = 9 – 20 + 18 – 7 + 1 = 1), si le point redevient un cube « parallèle » au premier (un hypercylindre), on obtient :
(a0 – 1 + 8) ‒ (a1 + 12) + (a2 + 6) ‒ (a3 + 1) + a4
= (9 – 1 + 8) – (20 + 12) + (18 + 6) – (7 + 1) + 1 = 1.
Procédons de même à partir d’un tétraèdre (pour lequel a0 ‒ a1 + a2 ‒ a3 = 4 – 6 + 4 – 1 = 1), en ajoutant un point dans la quatrième dimension pour former un hypercône (nommé pentachore). On aboutit à :
(a0 + 1) ‒ (a1 + 4) + (a2 + 6) ‒ (a3 + 4) + 1 = (4 + 1) – (6 + 4) + (4 + 6) – (1 + 4) + 1 = 1.
Le pentachore.
À partir de là (a0 ‒ a1 + a2 ‒ a3 + a4 = 5 – 10 + 10 – 5 + 1 = 1), si le point devient un tétraèdre « parallèle » au premier (un hypercylindre), on calcule que :
(a0 – 1 + 4) ‒ (a1 + 6) + (a2 + 4) ‒ (a3 + 1) + a4
= (5 – 1 + 4) – (10 + 6) + (10 + 4) – (5 + 1) + 1 = 1.
En dimension 4, un simplexe est un hypervolume dont les sommets se situent sur chacun des axes du repère orthonormé (O, x, y, z, w), plus l’origine O. Dans un espace de dimension n, on définit de même la notion de simplexe ; il s’agit d’un hypervolume dont les sommets se situent sur chacun des axes du repère orthonormé (O, x1, x2, x3… xn), plus l’origine O. Un simplexe possède donc n + 1 sommets.
En dimension 1, le simplexe est un segment ; on a : 2 – 1 = 1.
En dimension 2, le simplexe est un triangle ; on a : 3 – 3 + 1 = 1.
En dimension 3, le simplexe est un tétraèdre ; on a : 4 – 6 + 4 – 1 = 1.
En dimension 4, le simplexe est un pentachore ; on a : 5 – 10 + 10 – 5 + 1 = 1.
Pour les dimensions supérieures, il est facile de se convaincre que où désigne un coefficient binomial, à savoir le nombre de combinaisons de p objets pris parmi n.
En effet, il y a n + 1 sommets et chaque « élément » de dimension i du simplexe est obtenu par le choix de i + 1 sommets parmi tous les sommets.
On en déduit la relation fondamentale suivante :
En effet, on a
Ça commence avec un simplexe
La formule d’Euler est donc valide pour tout simplexe. Pour généraliser à tout polytope convexe de dimension n quelconque, ce simplexe de dimension n subit successivement diverses modifications, comme l’ajout ou l’« aplatissement » d’un sommet ou d’une arête. Sans prétendre à l’exhaustivité des possibilités, sept modifications sont présentées ci-après (pour faciliter la compréhension des phénomènes géométriques en jeu, les schémas représentent des polytopes tridimensionnels).
Sommet dupliqué d’un sommet départ de a arêtes : a0 augmente de 1, a1 augmente de 1 + 2 , a2 augmente de 2 (la répartition des a arêtes sur les deux sommets n’intervient pas).
Bilan : 1 – 3 + 2 = 0 ; la relation reste donc inchangée suite à cette opération.
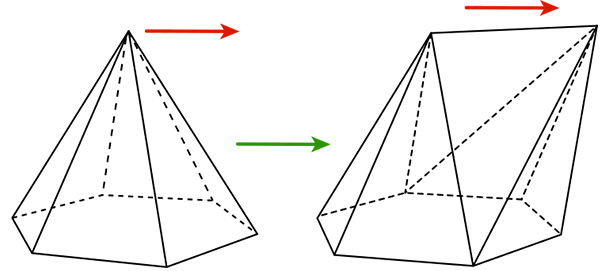
Sommet tiré d’une face ayant s sommets : a0 augmente de 1, a1 augmente de s, a2 augmente de s ‒ 1 (la face origine du point disparaît).
Bilan : 1 – s + (s – 1) = 0 ; la relation reste donc inchangée.

Sommet tiré d’une arête séparant deux faces avec s1 et s2 sommets, tout en restant dans le plan d’une des deux faces. L’entier a0 augmente de 1, a1 de s2 – 1 (une arête disparaît dans l’opération), a2 de (s2 – 1) – 1 (la face agrandie existait déjà ; l’autre face d’origine disparaît).
Bilan : 1 – (s2 – 1) + (s2 – 2) = 0.
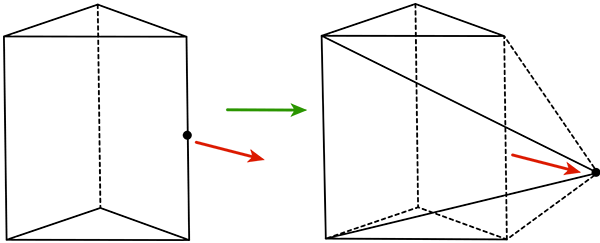
Sommet tiré d’une arête séparant deux faces ayant s1 et s2 sommets : a0 augmente de 1, a1 de s1 + s2 – 2 – 1 (deux sommets sont communs aux deux surfaces ; une arête disparaît), a2 de s1 + s2 – 2 – 2 (deux sommets communs aux deux surfaces ; les deux faces d’origine disparaissent).
Bilan : 1 – (s1 + s2 – 3) + (s1 + s2 – 4) = 0.
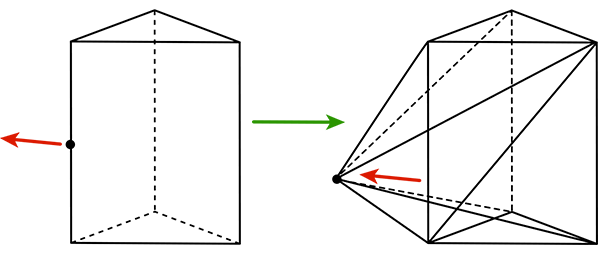
Une arête est tirée : ses extrémités sont issues de deux arêtes appartenant à la même face. On a a0 qui augmente de 2, a1 qui augmente de 1 + 2 (les arêtes d’origine sont brisées), et a2 qui augmente de 2 – 1 (une face disparaît).
Bilan : 2 – (1 + 2) + (2 – 1) = 0.

Un sommet (d’où partent a arêtes) est aplati : a0 augmente de a – 1 (un sommet disparaît), a1 augmente de a, a2 augmente de 1.
Bilan : a – 1 – a + 1 = 0.
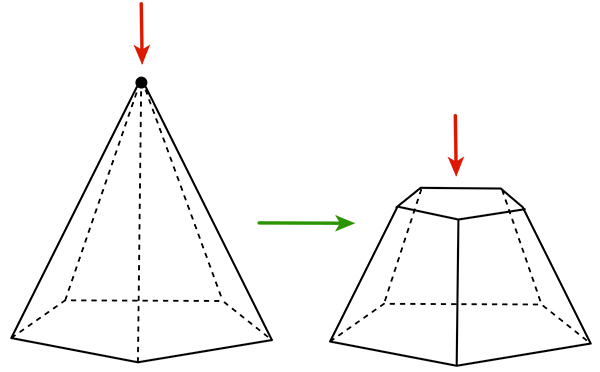
Une arête, dont les extrémités sont des sommets d’où partent a1 et a2 arêtes, est aplatie : a0 augmente de a1 + a2 – 2 – 2 (deux sommets disparaissent), a1 de a1 + a2 – 2 – 1 (deux arêtes sont communes ; une arête disparaît), et a2 de 1.
Bilan : (a1 + a2 – 4) – (a1 + a2 – 3) + 1 = 0.

Ici, a1 = a2 = 3.
Tout polytope a son dual
Il est possible d’interchanger les nombres de sommets et de faces (la figure présente l’exemple du cube). Les points centraux de chaque face du cube (polyèdre primal) sont les sommets du polyèdre dual. Chacun de ces sommets est l’intersection d’autant de faces que la face d’origine du cube a de sommets. Le dual d’un cube est un octaèdre, et réciproquement. Le cube a en effet huit sommets, douze arêtes et six faces, quand l’octaèdre possède six sommets, douze arêtes et huit faces.
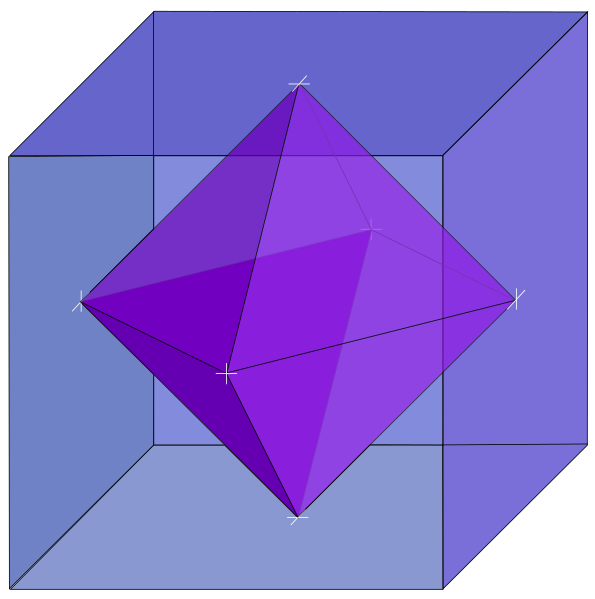
Polyèdre primal et polyèdre dual
avec l’exemple cube‒octaèdre.
Le dual d’un tétraèdre (lequel possède quatre sommets, six arêtes et quatre faces) est un tétraèdre. Le dual d’un icosaèdre (douze sommets, trente arêtes et vingt faces) est un dodécaèdre (vingt sommets, trente arêtes et douze faces), et réciproquement.
À partir de la dimension 4, le passage au polytope dual se présente comme une inversion de l’ordre des n – 1 premiers coefficients ai. Ainsi, le n-uplet (a0, a1… ak … an‒2, an‒1) devient (an‒1, an‒2… an‒k‒1 … a1, a0). Le polytope dual du tesseract (qui possède seize sommets, trente-deux arêtes, vingt-quatre faces et huit chores) est l’hexadécachore ou 16-cellules (polytope constitué de huit sommets, vingt-quatre arêtes, trente-deux faces et seize chores). La formule d’Euler reste vraie pour ces deux objets géométriques.
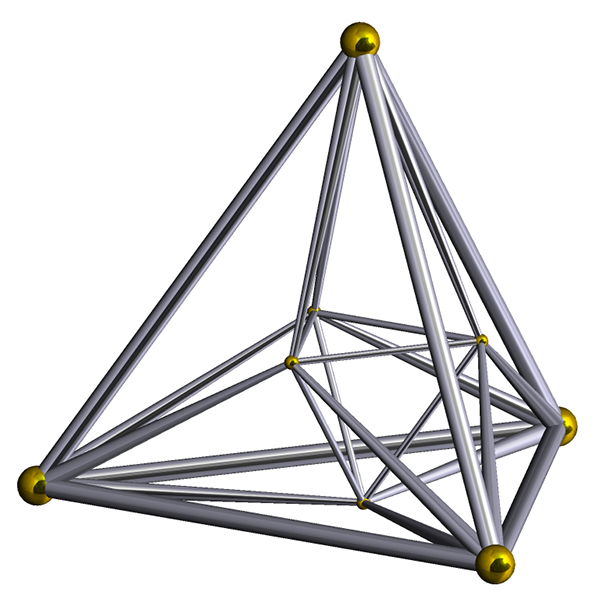
Représentation d’un hexadécachore.
L’icositétrachore (avec ses vingt-quatre sommets, ses quatre-vingt-seize arêtes, ses quatre-vingt-seize faces et ses vingt-quatre chores) est son propre dual. L’hécatonicosachore (600, 1 200, 720, 120) et l’hexacosichore (120, 720, 1 200, 600) sont duaux l’un de l’autre.
Application à la programmation linéaire
La notion de dualité se retrouve dans la technique de résolution de problèmes appelée programmation linéaire. Aussi connue sous le nom d’algorithme du simplexe, elle a été introduite à partir de 1947 par le mathématicien américain George Bernard Dantzig (1914‒2005). Le problème est posé sous forme d’une suite d’inégalités exprimant des contraintes (valeurs imposées maximales ou minimales), chacune liant linéairement les variables du problème (le mot « simplexe » prend tout son sens quand on ajoute des variablesd’écart pour transformer les inégalités en égalités, c’est-à-dire en passant de la forme canonique à la forme standard). Les contraintes représentent des hyperplans du polytope dont les sommets correspondent aux variables du problème. Une combinaison linéaire des variables doit être maximisée (ou minimisée) ; c’est la fonction de coût, qui correspond à un hyperplan indépendant du polytope. La solution se trouve donc sur un sommet du polytope (là où la fonction de coût est au top !). L’algorithme parcourt alors les arêtes du polytope dans un ordre judicieux pour atteindre « la » solution le plus rapidement possible. C’est le problème primal.
Le problème réalisé en transformant les variables du problème primal en contraintes et réciproquement (donc les sommets en hyperplans et réciproquement) s’appelle le problème dual et sa fonction de coût donne la même valeur optimale ! Le solveur (algorithme résolvant ce type de problème déclaratif) peut, quand bon lui semble, passer du problème primal au problème dual, et inversement.
Une fois les inégalités remplacées par des égalités (forme standard), les problèmes primal et dual ont bien le même nombre de variables. Ce nombre (la dimension du simplexe) est égal au nombre de contraintes, après la prise en compte de l’encadrement des variables (positivité par exemple). Dans la pratique, le nombre de variables pour ce type de problèmes est très… variable, allant de quelques dizaines à quelques milliers, voire beaucoup plus pour certaines applications.

