Essayez, à la règle et au compas, de construire un triangle connaissant les longueurs de ses trois côtés. Vous vous heurtez vite à des cas d’impossibilité liés à l’inégalité triangulaire, qui, comme son nom l’indique, constitue une « obligation » dans le triangle. D’autres inégalités peuvent avoir une interprétation géométrique simple ; l’inégalité arithmético-géométrique est l’une d’elles. Certaines, plus compliquées, sont même purement géométriques.
L’inégalité triangulaire
L’inégalité fondamentale du triangle.
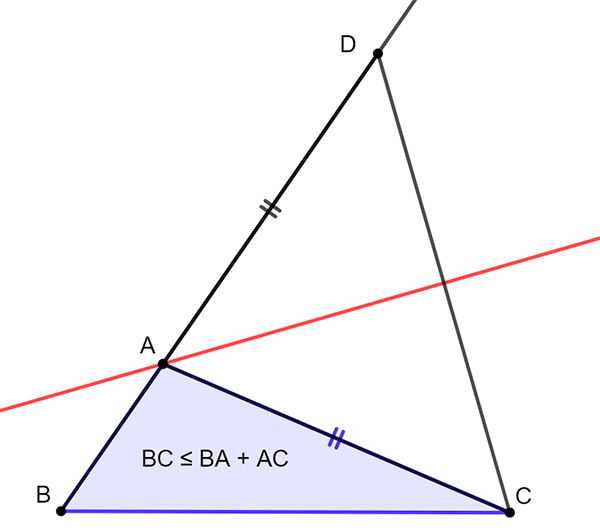
La ligne droite est, dit-on, le plus court chemin d’un point à un autre. Ainsi, dans un triangle ABC, aller de B à C selon le segment [BC] serait plus court qu’en passant par A. Est-ce vrai ?
Considérons le point D de la demi-droite [BA) tel que AD = AC.
B et D étant de part et d’autre de la médiatrice (en rouge) de [CD], B est plus proche de C que de D. Alors BC ≤ BD. C’est dire que BC ≤ BA + AD, soit BC ≤ AB + AC (1). L’adage dit donc vrai ; c’est ce que les mathématiciens appellent l’inégalité triangulaire. En d’autres termes, dans un triangle, la longueur d’un côté est inférieure ou égale à la somme des deux autres. Écrite ici pour une somme, cette inégalité ... Lire la suite