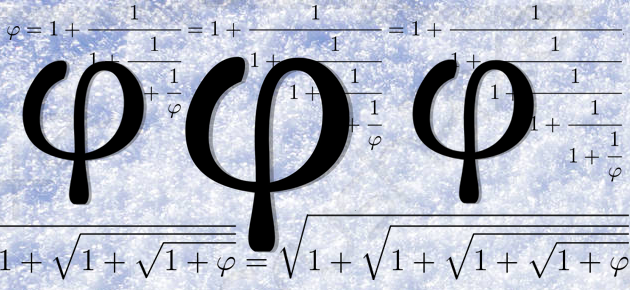
Le nombre d’or est souvent noté avec la lettre grecque φ (« phi »). Il s’agit sans doute d’une référence au sculpteur grec Phidias (vers − 490 ; vers − 430), dont l’influence fut considérable et à qui on doit peut-être les sculptures du Parthénon à Athènes. C’est le symbole qui sera adopté dans ce dossier pour désigner le nombre d’or. D’autres auteurs le désignent avec la majuscule Φ ou par une autre lettre grecque, τ (« tau »).
L’une des manières les plus élégantes de nos jours pour définir φ est de dire que c’est la solution positive de l’équation polynomiale du second degré suivante : x2 − x − 1 = 0.
Si on la calcule à l’aide des fameuses formules du trinôme, on trouve dont une valeur approchée à 10 −6 près est 1,618034. On peut, bien sûr, en calculer une valeur approchée avec autant de décimales que l’on veut, mais le nombre réel
étant un nombre irrationnel (il ne peut pas s’écrire comme un quotient de deux entiers) l’écriture décimale de φ ne peut pas être finie, ni être périodique à partir d’un certain rang (comme peut l’être, par exemple, 0,892857142 85714285714… où la suite des chiffres « 285714 » se reproduit indéfiniment après ... Lire la suite
