
Voici son énoncé tel que le pose Euler :
« Trente-six Officiers de six différens grades et tirès de six Régimens différens, qu’il s’agissoit de ranger dans un quarré, de manière que sur chaque ligne tant horizontale que verticale il se trouva six Officiers tant de différens caractères que de Régimens différens. »
Une idée qui deviendra classique
Euler se lance alors dans l’étude de ce qu’il appellera les carrés gréco-latins. Un carré latin d’ordre n est un carré de n2 cases dont on remplit les cases avec les n premières lettres de l’alphabet latin, de telle sorte que dans chaque ligne et dans chaque colonne, les lettres soient toutes différentes.
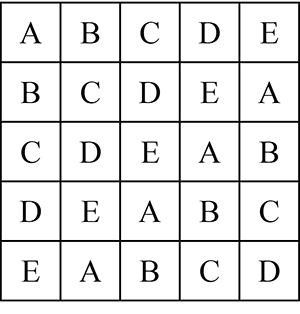
Un carré latin d’ordre 5.
Un carré gréco-latin d’ordre n est un carré contenant les n premières lettres de l’alphabet latin et les n premières lettres de l’alphabet grec, chaque case contenant une lettre de chaque alphabet de sorte qu’une même lettre, latine ou grecque, ne figure jamais deux fois dans une même ligne ou une même colonne, et que les couples (lettre latine ; lettre grecque) soient tous différents.

Un carré latin d’ordre 5 avec des lettres grecques.
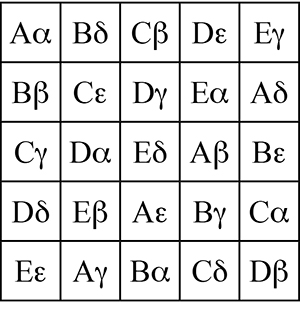
Un carré gréco-latin d’ordre 5.
Si deux carrés permettent de construire un ...
Lire la suite
