
Le triangle de Penrose
C’est le cas du triangle de Penrose, appelé aussi tribarre ou tripoutre, constitué de trois poutres liées entre elles et représentées en 2D. Avec son père, Lionel Penrose (1898 —1972), ils en publièrent le dessin dans un article du British Journal of Psychology en février 1958. Roger Penrose en avait eu l’idée après avoir découvert le travail du graveur néerlandais Maurits Cornelis Escher (1898—1972) alors qu’il se trouvait à Amsterdam en 1954 pour le Congrès international des mathématiciens.
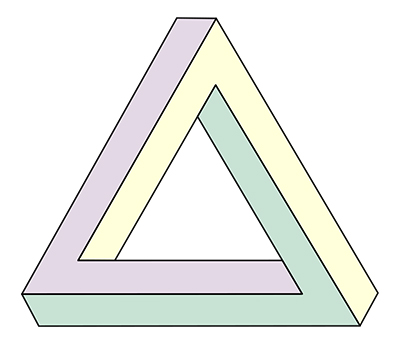
Le triangle de Penrose.
En fait, c’est l’artiste suédois Oscar Reutersvärd (1915—2002) qui, le premier, a dessiné une série de neuf cubes dans la même configuration. C’était en 1934 pendant un cours de latin où, selon ses dires, il s’ennuyait.
Cette découverte changea le cours de sa vie. Au cours de sa carrière de graphiste, il dessina de très nombreuses « figures impossibles » : il est d’ailleurs parfois surnommé le « père de l’impossible ». Pour lui rendre hommage, la Suède a émis en 1982 une série de timbres.

Les timbres suédois en hommage à Reutersvärd.
Manifestement, ni les Penrose, ni Escher n’avaient eu connaissance des figures créées, des années auparavant, par Reutersvärd.

Représentation de l’illusion de Reutersvärd
(devinez l’astuce mise en œuvre pour la réalisation !).
L’escalier de Penrose
Une autre « figure impossible » est présente dans l’article écrit par les Penrose en 1958 : l’escalier. Mais, là encore, cette figure avait déjà été décrite par Reutersvärd, en 1937 !
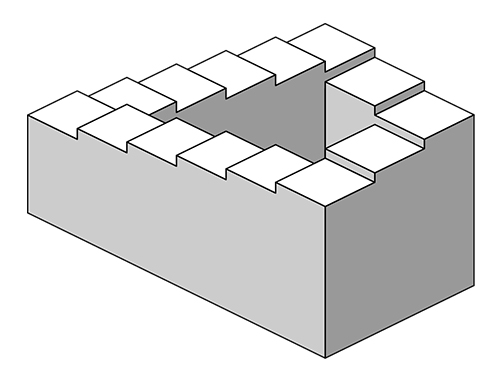
L’escalier de Penrose.
Escher a connaissance de cet objet suite à des échanges avec Roger Penrose. Dès 1960, il en tirera une lithographie restée célèbre, Montée et Descente. Andrew Lipson et Daniel Shiu ont réussi à recréer cette œuvre (et bien d’autres, voir le site, http://www.ams.org/publicoutreach/math-imagery/lipson ) avec des briques danoises…

Réalisation avec des briques danoises de l’œuvre Montée et Descente d’Escher (trouvez l’artifice que les artistes ont utilisé !).
Références :
Maths et arts plastiques. Bibliothèque Tangente 23, 2018.
Inventions mathématiques. Jean-Paul Delahaye, Pour la Science, 2014.
Les secrets des dimensions. Bibliothèque Tangente 66, 2019.
