
De nombreux ouvrages rédigés
Mary Everest (1832 −1916) rencontre George Boole en 1850. Il était devenu en quelque sorte son tuteur en mathématiques, elle qui n’avait pas eu le droit de les étudier, puisque l’université était fermée aux filles. Ils se marient en 1855. À la mort de George, en 1864, elle a la charge de ses cinq filles et doit exercer divers petits métiers. Elle est amenée à enseigner les mathématiques, notamment au Queen’s College, créé pour former en particulier les futures « nurses ».

Mary adore enseigner et invente des méthodes très novatrices, trop probablement pour son époque. Dès 1889, elle commence à écrire de nombreux ouvrages de pédagogie des mathématiques, où se mêlent aussi la religion, la philosophie, un peu d’ésotérisme, ce qui n’en rend pas la lecture très facile. Les titres en sont très évocateurs : Logic taught by love en 1889, The cultivation of the mathematical inspiration en 1902, Lectures on the logic of arithmetic en 1903, The preparation of the child for science en 1904, Philosophy and fun of algebra en 1909, Some master keys of the science of notation en 1911. La liste est en fait fort longue !
Lors de l’écriture de l’œuvre majeure de son mari, les Lois de la pensée, ils ont beaucoup échangé sur la façon de penser les mathématiques. George Boole était lui-même passionné par la pédagogie des mathématiques et puisait dans sa propre expérience d’autodidacte. Mary consacra sa vie à la diffusion des idées de son époux ; ses méthodes pédagogiques étaient l’un de ces moyens.
Le calcul différentiel par la couture
Les idées de Mary Everest Boole sur l’enseignement incluent le jeu dès le plus jeune âge et la manipulation d’objets (sphères, cubes, cônes, bûchettes…). Sa grande invention est le curve stitching, ou « cartes à coudre », connu aussi sous le terme « tableau de fils », à utiliser dès le jardin d’enfants et jusqu’à l’université. Cela permet de se poser des questions sur les courbes, d’en imaginer, de manipuler des nombres et les opérations, de penser les dimensions 2 et 3, voire même 4, et surtout peu à peu d’arriver aux notions de calcul différentiel, d’équation de courbe…
Mary précise qu’il est beaucoup plus facile de tracer des droites avec un fil et une aiguille qu’avec une règle, ajoutant malicieusement que les garçons comme les filles apprenaient les mathématiques en cousant ! Ses idées sont reprises dans des manuels contemporains pour l’enseignement de l’analyse. Mais elles sont aussi beaucoup utilisées dans le domaine artistique.
Les courbes du string art
Nées au XIX e siècle de l’imagination de Mary Everest Boole, des créations artistiques faites de clous et de ficelles tendues se sont popularisées sous le nom de string art.

Une cardioïde en string art.
Elles permettent d’engendrer de jolies courbes, définies comme étant tangentes à toutes les droites d’une même famille, donc enveloppes d’un ensemble de droites. Un modèle simple est celui de l’enveloppe des cordes d’un cercle. Si l’on a par exemple disposé sur ce cercle (de rayon 1) des clous numérotés (de 1 à 24) correspondant à des angles au centre de 15°, et qu’on tend entre les clous 1 et 2, 2 et 4, 3 et 6… des ficelles, on voit apparaître une courbe en forme de cœur tangente à toutes les cordes de ficelle. Les cordes ainsi construites sont en fait des droites passant par les points A(cos t, sin t) et B (cos 2t, sin 2t) et la courbe qui se dessine est l’enveloppe des droites de cette famille. Elle a pour équations paramétriques
il s’agit d’une cardioïde de point de rebroussement de coordonnées (−1/3, 0).
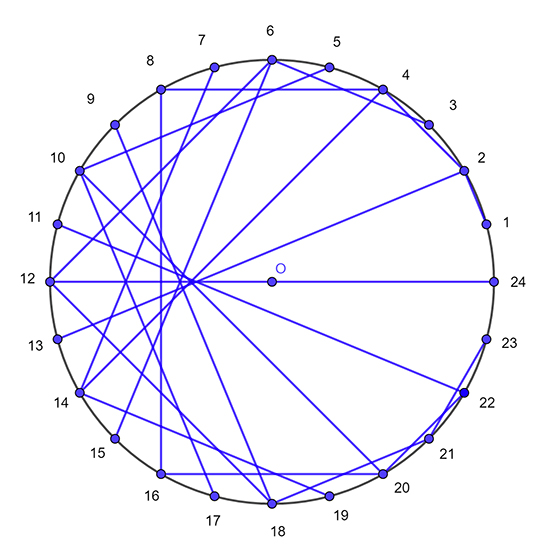
Naissance d’une cardioïde.
