
Considérons tous les points du plan et attribuons à chacun d’entre eux une couleur de façon à ce que deux points quelconques distants d’une unité soient de couleur différente.
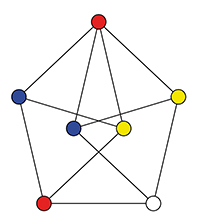
En considérant un triangle équilatéral de côté 1, on s’aperçoit que deux couleurs ne suffisent pas à colorer tous les points du plan. En fait, trois couleurs non plus, comme le montre le graphe de Moser (ci-dessous).
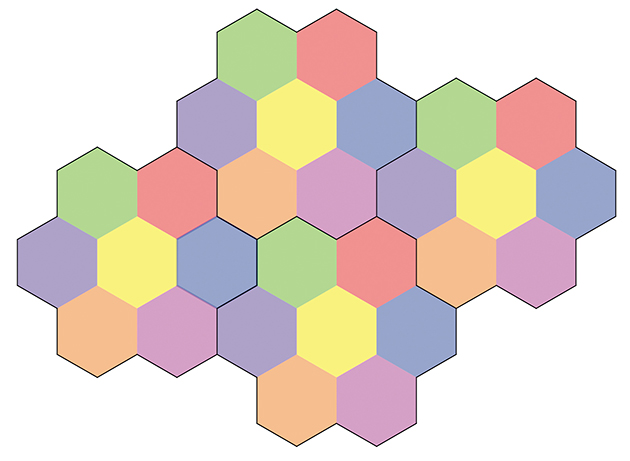
Par ailleurs, sept couleurs suffisent. Pour s’en rendre compte, on peut paver le plan avec des hexagones de diamètre légèrement inférieur à une unité.
Une question se pose alors : quel est le nombre minimum de couleurs nécessaires ? Quatre, cinq, six ou sept ? La réponse n’est pas simple. Il a fallu attendre avril 2018 pour que Aubrey de Grey, un biologiste britannique spécialiste du vieillissement mais aussi mathématicien amateur, propose un graphe constitué de segments de longueur 1 et nécessitant cinq couleurs ! Le graphe en question compte plus de vingt mille sommets mais il a depuis été simplifié et on tient maintenant un exemple à un peu plus de huit cents sommets (seulement). Alors, cinq, six ou sept couleurs pour colorer le plan ?
