
La formule d’Euler affirme que, pour un polyèdre, sous certaines conditions, si S désigne le nombre de sommets, F le nombre de faces et A le nombre d’arêtes, on a la relation
S + F – A = 2.
Elle est extraordinaire à plus d’un titre (voir le dossier consacré à cette formule dans Tangente 174, 2017). Extraordinaire de simplicité, elle lance un pont entre la géométrie (les polyèdres) et l’arithmétique (S, F et A sont des nombres entiers). Elle introduit en outre la notion de dualité…

On lit souvent que le tétraèdre est « son propre dual ». En fait, le dual du tétraèdre est un autre tétraèdre. Dans l’opération de dualité, on fait correspondre à un sommet une face. Plus précisément, à un sommet où convergent n faces et n arêtes, on peut faire correspondre une face possédant n côtés, et réciproquement (à une face à m côtés on peut faire correspondre un sommet où convergent m faces et arêtes).
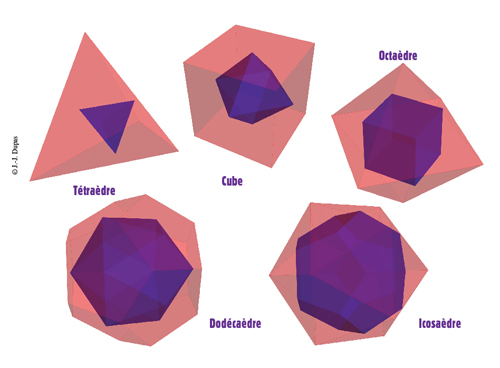
Les solides de Platon et leurs polyèdres duaux.
Pour les solides de Platon, la recette pour obtenir le polyèdre dual est assez simple : il suffit de prendre les centres des faces. Le polyèdre dual est alors ... Lire la suite
