
Une « formule de Héron » en 3D par Euler
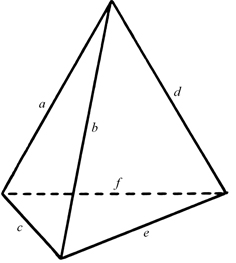 Comme c’est le cas pour le triangle dans le plan, un tétraèdre est entièrement déterminé par la longueur de ses six arêtes. Aussi, existe-t-il une formule analogue à celle de Héron pour le tétraèdre ?
Comme c’est le cas pour le triangle dans le plan, un tétraèdre est entièrement déterminé par la longueur de ses six arêtes. Aussi, existe-t-il une formule analogue à celle de Héron pour le tétraèdre ?
Oui, et c’est le grand mathématicien suisse Leonhard Euler (1707–1783), s’inspirant apparemment de travaux de Tartaglia à la Renaissance, qui a mis à jour une telle formule pour un tétraèdre. Dans cette relation, a, b, c, d, e et f sont les longueurs respectives des arêtes du tétraèdre, l’arête a étant opposée à e, l’arête c à d et l’arête b à f. Le volume du tétraèdre (analogue à l’aire du triangle dans le cas du plan) est noté V. On a donc :
122 V2 = (a 2e 2 + b2 f 2 + c 2d 2)(a 2 + b 2 + c 2 + d 2 + e 2 + f 2) – 2(a 2e 2 (a 2 + e 2)
+ b 2f 2(b 2 + f 2)+ c 2d 2(c 2 + d 2)) – (a 2b 2d 2 + a 2c 2f 2 + b 2c 2e 2 + d 2e 2f 2).
On ne peut qu’admirer la puissance de travail légendaire et l’intuition du grand Euler, qui lui ont sans doute permis de trouver une telle formule à une époque où les seuls outils du mathématicien ... Lire la suite gratuitement
