
L'aventure mathématique se niche parfois là où on ne l'attend pas, comme au détour… d'une toile d'araignée. Tout commence avec un carré servant de cadre à la toile. L'arachnide se trouve initialement sur le côté gauche en A0, puis va rejoindre les milieux des côtés adjacents en tournant dans le sens des aiguilles d'une montre. D'accord, une vraie araignée ne s'y prendrait pas comme cela (voir Mathématiques et Biologie, Bibliothèque Tangente 42), mais ici nous avons affaire à une araignée mathématique ! Cette construction en vaut d'ailleurs bien une autre et sa récurrence géométrique simple permet de se changer les idées.
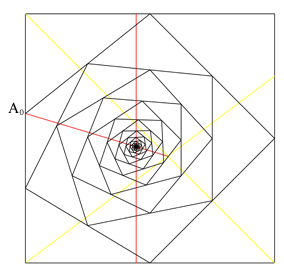
En avançant dans le tracé, force est de constater que l'araignée se dirige vers un point bien précis sur sa toile. En d'autres termes, on dirait qu'elle converge ! C'est la porte d'entrée d'une investigation qui va nous promener agréablement dans le paysage… de l'algèbre linéaire.
L'espace vectoriel des toiles
 La suite des points (An)n est parfaitement déterminée par la suite de leurs affixes (zn)n, obtenue en immergeant le cadre carré de la toile d'araignée dans le carré du plan complexe délimité par O, 1, i, i + 1. On choisira O pour l'affixe du sommet ... Lire la suite gratuitement
La suite des points (An)n est parfaitement déterminée par la suite de leurs affixes (zn)n, obtenue en immergeant le cadre carré de la toile d'araignée dans le carré du plan complexe délimité par O, 1, i, i + 1. On choisira O pour l'affixe du sommet ... Lire la suite gratuitement
