
«À quoi ça sert les maths ? » « Les maths c'est trop abstrait ! » « C'est quoi une fonction ? » Autant de questions que les enseignants entendent souvent… et qui sont pertinentes ! C'est la raison pour laquelle la mise en évidence des liens entre ce que les élèves étudient au lycée et le monde qui les entoure peut permettre de mieux comprendre les mathématiques. La calculatrice Graph 90+E est dotée d'un menu (Plot Image) créé pour aider les élèves à faire ce lien.
Appréhender une trajectoire
L'intérêt du menu Plot Image est de pouvoir placer sur une image des points qui vont permettre de mettre en exergue des courbes et des formes géométriques pour pouvoir les étudier. Il est aussi possible de travailler sur des images animées ou des films. Pour cela, on va découper la séquence de film étudiée en un nombre d'images égal au nombre de points à placer. À chaque fois que l'on placera un point, l'image passera à la suivante. Il est ainsi possible de suivre, entre autres phénomènes, la trajectoire d'un objet.
Intéressons-nous à la célèbre scène du globe du film satirique le Dictateur de Charlie Chaplin (Charles Chaplin Productions, 1940), classique du septième art s'il en est. Cette scène a été maintes fois analysée, mais elle va faire ici l'objet d'un tout autre regard : il va s'agir d'étudier la trajectoire du globe lorsque le dictateur joue avec. La scène a été au préalable découpée en dix images, que l'on peut ensuite transférer à la calculatrice avec un simple câble USB. Vous pouvez télécharger ce fichier et trouver plus d'informations sur cette activité sur le site casio-education.fr, rubrique « La Pédagogie ». Titre de la ressource : « Le polynôme de Charlie Chaplin », téléchargeable gratuitement.
Le problème du repérage
Pour modéliser la trajectoire du globe, plaçons des points sur chacune de ses positions. Commençons par observer les différentes images :
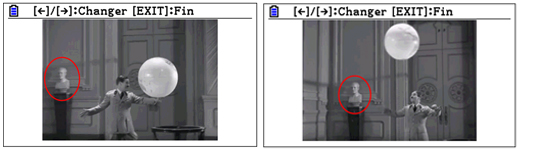
On observe que le cadrage du cameraman change : sur la première image, la statue est complètement sur la gauche, mais sur la deuxième, la statue n'est pas tout à fait au même endroit. Pour pallier ce problème, il va falloir positionner l'origine du repère au milieu de la tête de la statue sur chaque image.
Construction des points
On place les points qui correspondent à la position du globe sur chacune des images. Pour plus de précision, nous prenons toujours le pôle Sud du globe. On obtient l'image ci-dessous.

Interpolation par un polynôme du second degré
La trajectoire ressemble à une parabole. Il s'agit alors de construire la représentation graphique du polynôme P(x) = a(x – k)2 + h et de faire varier les paramètres a, k et h pour que la parabole passe « au plus près possible » des points. Cela permettra de voir le lien entre les paramètres de la forme canonique d'un polynôme du second degré, les coordonnées du sommet de la parabole et les variations de la fonction. Par exemple, avec un choix des paramètres de 1, 2,9 et 1,6 respectivement, on obtient P(x) = –(x – 2,9)2 + 1,6, soit encore P(x) = –x2 + 5,8 x – 6,81. Ce choix conduit à la figure ci-dessous (parabole en bleu), qui n'est pas très satisfaisante.

Régression
Vérifions maintenant notre résultat avec la régression quadratique de la calculatrice :On observe que nous avons manqué de précision lors de la phase d'approximation « manuelle », mais que même la régression quadratique de la calculatrice n'est pas très satisfaisante. Construisons maintenant une régression de degré 3 (en bleu sur la capture d'écran ci-dessous).
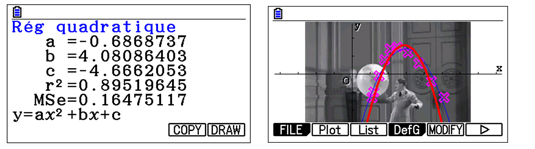
On constate que cette courbe est beaucoup plus satisfaisante. Elle peut aussi être un bon moyen d'introduire les régressions, et de voir expérimentalement que plus le degré du polynôme est grand, plus l'approximation est précise. On pourrait d'ailleurs tout aussi bien tester d'autres types de régression : les portes de l'expérimentation sont grand ouvertes…

