
Les sommes d'entiers en images
Les agencements visuels de points se prêtent à merveille à illustrer la variété des preuves sans mots (voir la note de lecture ci-dessus). L'assemblage suivant, par exemple, popularisé par Martin Gardner, illustre que la somme des n premiers entiers est égale à n (n + 1) / 2.


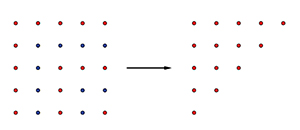
Un autre classique a rencontré beaucoup de succès sous la plume de John Horton Conway et Richard Kenneth Guy (le Livre des nombres, Eyrolles, 1998). Il s'agit de la preuve visuelle que la somme des n premiers entiers impairs est égale à n2.
Enfin, relatée dans le livre de Roger Nelsen, la somme alternée des carrés d'entiers s'exprime algébriquement ainsi :
Cette égalité peut être traduite visuellement par le joli dessin suivant, dû au mathématicien américain Steven Snover :
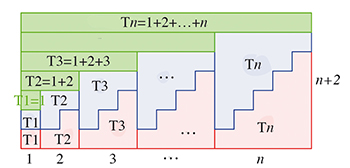
La somme des nombres triangulaires
Un bel exercice de pavage est relaté par Roger Nelsen dans l'ouvrage mentionné ci-dessus. Il est dû à l'ingéniosité de Monte Zerger, mathématicien américain à la retraite, et nous propose de revisiter l'égalité classique concernant la somme des n premiers entiers. Sauf que dans cette interprétation, la formule invite à réfléchir sur la somme des n premiers nombres triangulaires (c'est-à-dire de la forme k (k + 1) / 2, avec k un entier).
Émotions visuelles et réflexion mathématique
Les « preuves sans mots » sont, nous dit l'auteur, des « figures, schémas ou diagrammes qui aident le lecteur à comprendre pourquoi un énoncé mathématique particulier peut être vrai, ainsi qu'à voir comment on pourrait tenter de le démontrer ». Aux esprits chagrins qui disent qu'une « preuve visuelle » n'est pas une preuve, on peut dire, à la lecture de ce livre, que les preuves visuelles de Roger Bain Nelsen ont toutes le mérite de faire réfléchir… et même parfois longuement, et mettent sur la voie d'une véritable démonstration. Cette dernière peut se faire, dans le cas de preuves géométriques, par dissection-recomposition, ou, dans le cas de preuves algébriques, par un calcul associé au dessin. Attention toutefois à bien interpréter les notations des dessins, pas toujours très clairement disposées !
Deux phénomènes étonnants : le grand nombre de preuves présentées (plus de deux cent trente), et la variété des domaines abordés : géométrie (avec par exemple treize puzzles de Pythagore) et algèbre, trigonométrie, géométrie analytique, calcul différentiel et intégral, très nombreuses inégalités, combinatoire et sommes d'entiers, suites et séries et même quelques thèmes d'algèbre linéaire. Ce livre offre donc une vaste palette de sujets donnant matière à de beaux exercices, tant pour élèves que pour étudiants ou simplement pour amateurs curieux d'émotions visuelles.

