La dérivée logarithmique
Dériver le logarithme népérien d'une fonction f dérivable à valeurs strictement positives peut parfois simplifier certains calculs. Cette nouvelle dérivée a un nom : c'est la dérivée logarithmique ; elle est formellement définie par L( f ) = f ‘ / f.
Elle vérifie des propriétés remarquables : si g est une autre fonction dérivable valeurs strictement positives, alors
•
•
• si α > 0 est un exposant réel, L(f α) = (f α f ') / f α = α L(f), relations fonctionnelles qui ne sont évidemment pas sans rappeler les propriétés du logarithme…
La spirale logarithmique
La spirale logarithmique, que l'on rencontre si souvent dans la nature, sur les coquilles de coquillages, dans le cœur des fleurs de tournesol ou dans la forme des galaxies, est une courbe plane d'équation polaire r = aem θ où a est un réel positif et m un réel non nul. C'est la trajectoire d'un point M se déplaçant sur une droite passant par O avec une vitesse proportionnelle à OM, la droite tournant autour de O à vitesse constante. Étudiée par Descartes et Torricelli, elle a même fait l'objet d'un ouvrage complet de Jacques Bernoulli en 1691, qui la nommait « spira mirabilis » et qui en a fait graver une sur sa tombe. Cette courbe possédait selon lui tant de propriétés d'invariance qu'elle méritait la maxime « Eadem mutata resurgo » (« Je renais à l'identique »).

Il est vrai que cette courbe coupe par exemple tous ses rayons vecteurs sous un même angle et qu'elle est invariante par une similitude d'angle θ 0 et de rapport e m θ0 . Dommage que le sculpteur ait gravé une spirale d'Archimède (d'équation polaire r = k θ)…
Spirale « presque » logarithmique sur le tombeau de Jacques Bernoulli à Bâle.
Les échelles logarithmiques en science
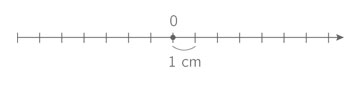
Pour graduer une droite D, on peut utiliser une échelle linéaire qui, une fois choisie une origine O, fait correspondre à tout point M de D le réel t, son abscisse, proportionnel à la distance OM. Ici, deux graduations dont les différences sont égales sont à distance constante.
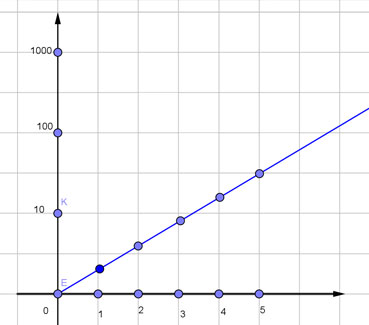
On peut aussi, surtout dans le cas d'une grande amplitude de valeurs, définir une échelle logarithmique qui, à tout point M de D, associe le réel t tel que le logarithme de t (dans une base quelconque, mais on choisit souvent la base 10, donc le logarithme décimal) soit proportionnel à la distance OM. Là, deux graduations dont les rapports sont identiques sont à distance constante.
Pour un repère plan, on peut aussi graduer l'un des axes selon une échelle linéaire, l'autre selon une échelle logarithmique : on obtient alors une échelle semi-logarithmique. Ainsi, des taux de croissance identiques sont représentés par des segments de même inclinaison sur l'axe des abscisses.
Les échelles logarithmiques sont omniprésentes en sciences. Le pH en chimie est défini par –log C, où C représente la concentration en ions H3O+ d'une solution. En acoustique, le niveau sonore S, mesuré en décibels, est égal à 10 log(I/I0) où I est l'intensité sonore et I0 une intensité de référence, celle du seuil d'audibilité de l'oreille humaine. La célèbre « échelle de Richter », introduite en 1935 en sismologie, décrivant la magnitude M d'un tremblement de terre, s'exprime de manière similaire : M = log(I/I0) où I est l'intensité du séisme étudié et I0 une intensité de référence. La magnitude M des étoiles en astronomie, égale à log(E/E0) où E est l'éclat de l'astre étudié et E0 un éclat de référence, est elle aussi un exemple courant d'échelle logarithmique.