La démonstration d'Euclide décortiquée

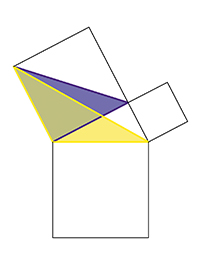
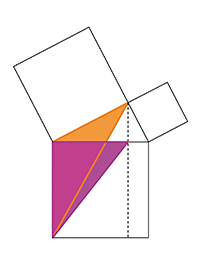
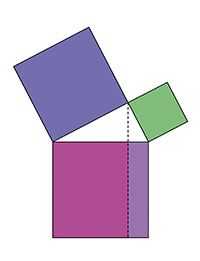
Si on veut démontrer avec rigueur le théorème de Pythagore, cela peut demander quelques lignes. La subtile démonstration due à Euclide (proposition 47 du livre I) n'est pas si difficile à suivre : sur les figures ci-dessous, les triangles bleu, jaune, orange et rose ont la même aire. On en déduit que le carré bleu a la même aire que le rectangle rose. Il en est de même du carré vert et du rectangle violet, ce qui achève la démonstration.

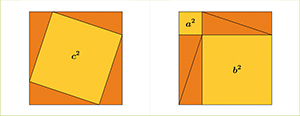
En fait, il s'agit bien souvent de trouver une configuration dans laquelle on démontre que l'aire d'un carré de côté c est égale à la somme des aires de deux carrés de côtés a et b.

Quelques découpages de génie

Parmi les nombreuses démonstrations du théorème de Pythagore, certaines se passent presque de commentaires. Elles se présentent souvent sous forme de puzzles où les pièces sont assemblées de deux façons différentes. Êtes-vous convaincus par les exemples ci-dessous ?

 Cette démonstration pourrait même se présenter sous la forme d'un puzzle articulé.

Voici un autre grand classique des preuves sans mots.

La construction suivante est moins connue. La droite coupe la figure en deux pentagones d'aires égales.

Enfin, cette dernière configuration est sans doute encore moins facile à retenir…