Même si leurs prévisions sont forcément imparfaites, les modélisations mathématiques des épidémies sont destinées à aider la décision en politique de santé. Plus précisément, quand une maladie prend une allure épidémique, les modèles tentent de répondre aussitôt que possible à la question : est-on en présence du début d'une épidémie ? Si oui, quelle sera son ampleur ?
Le modèle SIR
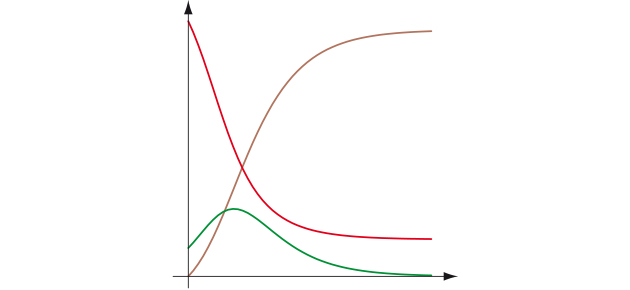
William Kermack et Anderson McKendrick ont proposé la première modélisation réaliste en 1927. Leur modèle compartimente la population en trois classes : S, la classe des individus susceptibles d'attraper la maladie, I, celle de ceux qui en sont infectés (et contagieux) et R, ceux qui en sont revenus ou sont morts. Dans les deux cas, ces derniers sont immunisés et ne contamineront plus personne. Le modèle SIR suppose implicitement que la population totale (P = S + I + R) n'augmente pas et il considère l'évolution de ces trois classes dans le temps en fonction de deux taux mesurables expérimentalement.
• Le premier (α) est le taux de contagion de la maladie pour un infecté, c'est-à-dire la probabilité qu'un individu susceptible attrape la maladie après contact avec un individu infecté, le nombre total de contacts étant censé être le produit ...
Lire la suite