Maple est un logiciel mathématique très complet. Ses capacités de calcul formel permettent d'obtenir des solutions exactes à de nombreux problèmes. Les possibilités de Maple sont illustrées par la résolution d'un problème d'optimisation.

 Connu pour être un puissant outil de calcul numérique et formel, Maple (Maplesoft) possède également des fonctions et interfaces interactives de visualisation graphique en 2D et 3D, d’Audio, et de Vidéo, très avancées. Ses packages, ses MathApps, et ses Tuteurs lui permettent d’aborder, illustrer, conjecturer, démontrer et comprendre de nombreux concepts mathématiques. L’environnement Maple peut être complété par le dispositif Maple T.A. dans lequel la construction de questions (éventuellement aléatoires) de différents types et de parcours pédagogiques suivis d’évaluation, constitue une vraie valeur ajoutée pour l’apprenant. Il est aussi un outil performant pour la pratique de pédagogies nouvelles, dont les classes inversées sont un exemple. Son apprentissage est rapide d’autant qu’une aide en ligne et des tutoriels accessibles en permanence dispensent quasiment de la lecture du manuel de l’utilisateur.

Maple réunit donc toutes les qualités pour expérimenter les mathématiques, c’est-à-dire pour aborder cette discipline d’ une manière originale, stimulante, vivante et propice aux découvertes et aux intuitions. Les multiples facettes de cet environnement sont illustrées par la résolution du problème d’optimisation qui suit.

 Découverte de l’optimisation

 L’optimisation est abordée comme application de la notion de dérivée. Maple en facilite la compréhension et l’enrichit en reliant les différents aspects. Considérons le problème suivant (une vingtaine de problèmes variés sur le thème de l’optimisation, avec les fichiers source Maple associés sont accessibles sur MapleCloud) :

 Quelles sont les dimensions du cylindre de volume maximal que nous pouvons inscrire dans une sphère de rayon 4 ?

 L’environnement Maple permet de planifier un travail préliminaire sous forme d’exploration pédagogique pour s’assurer de la maîtrise des prérequis. Grâce à Möbius, permettant la mise en ligne des cours et de leurs contenus pédagogiques interactifs, ce travail s’effectue aussi bien à distance qu’en présentiel. Les élèces pourront, par exemple :
— Revoir les propriétés des cylindres (patron, rotation d’un rectangle autour de l’un de ses côtés...), pour en tirer les différentes formules (volume, surface,..) en suivant des consignes vocales.

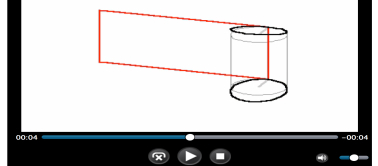
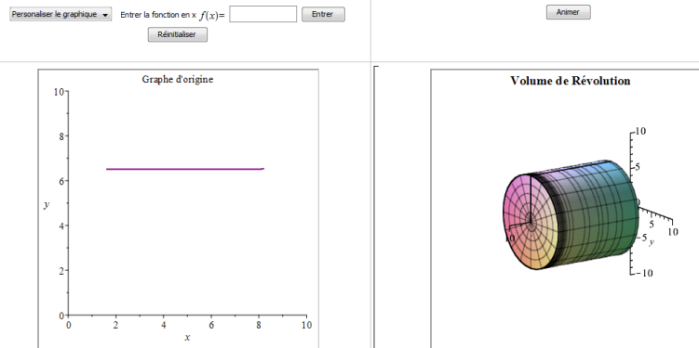
— Explorer la notion de solide de révolution, généré par la rotation de la fonction constante autour de l’axe grâce à la librairie des Math Apps. À noter qu’agir sur le code pour changer la langue de l’interface de l’application est facilement réalisable.

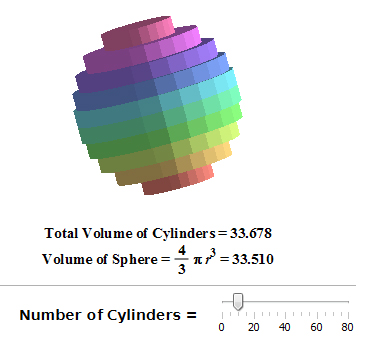
— Approcher d’une manière interactive le volume d’une sphère par des cylindres. Ce qui est une occasion d’aborder des notions telles que les limites et la convergence de suites.

Résolution du problème  

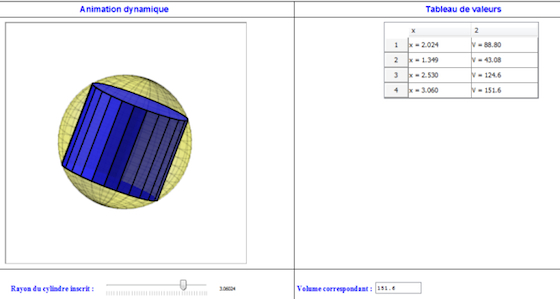
 Étape 1 : visualisation à l’aide une animation dynamique.

La création de plusieurs figures mobiles en 3D, contrôlées par les différentes variables du problème (ici la hauteur et le rayon du cylindre), améliore la perception spatiale de ces représentations.

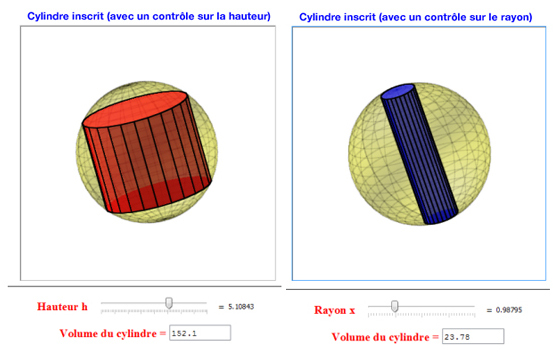
Étape 2 : résolution par tâtonnement.

Les figures dynamiques peuvent être associées à un tableau de valeurs. En contrôlant d’une manière interactive les variables du problème, l’apprenant est dans la capacité d’approcher numériquement la solution optimale.

Étape 3 : développement analytique.

L’analyse complète d’une fonction d’optimisation (domaine de définition, dérivées, monotonie, points remarquables, courbe) est possible, quelle que soit sa forme, soit en appelant directement les commandes , Maple, soit par le processus intuitif Mathématiques cliquables. L’outil Tuteurs permet de vérifier ses différents résultats en toute autonomie.
Dans notre exemple, le choix d’agir sur le rayon du cylindre (noté x) génère la fonction suivante à optimiser : x → 2πx2 −x2 + 16 Maple donne immédiatement l’expression algébrique de la dérivée et indique les racines.
Par ailleurs, plusieurs pistes alternatives sont facilement explorables avec Maple. Par exemple, élever la fonction au carré et vérifier graphiquement et analytiquement que son maximum a lieu e au même point que le maximum de sa fonction d’origine en est une belle illustration...

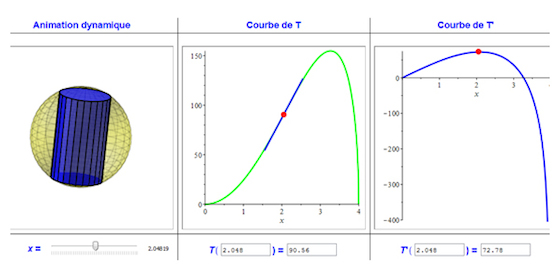
Étape 4 : synthèse visuelle.

Le graphe d’une fonction est souvent perçu comme un objet statique et son lien avec un phénomène n’est pas toujours facile à établir pour l’élève. La panoplie de composants interactifs Maple permet d’agir sur les différentes variables du problème pour illustrer simultanément plusieurs notions : la tangente (au niveau de la fonction), le signe (au niveau de la première dérivée) et la concavité (au niveau de la dérivée seconde).

Travailler d’une manière autonome l’ensemble des problèmes est nécessaire à la maîtrise des concepts. La plate-forme Maple T.A. propose un environnement adapté à la construction de parcours pédagogiques dirigés et évaluables, avec des rétroactions (feedback) simples ou personnalisées, on pourra donc aisément amener l’apprenant à construire lui-même toutes ces animations avec leurs synthèses visuelles.

Une vingtaine de problèmes variés sur le thème de l’optimisation, avec les fichiers source Maple associés sont accessibles sur MapleCloud.