
Interview de Victoria Callet

Dans quel domaine de recherche votre thèse s’inscrit-elle ?
Je travaille à l’Institut de recherche mathématiques avancées (IRMA) de Strasbourg et j’enseigne à l’Institut nationale des sciences appliquées (INSA) de cette même ville. Dans ma thèse, intitulée « Modélisation topologique des structures et processus musicaux » et dirigée par Moreno Andreatta et Pierre Guillot, j’ai étudié certains des liens qui existent entre l’algèbre et la musique. Plus précisément, mes domaines de recherches portent sur l’analyse topologique de certaines structures musicales via un outil simplicial appelé l’homologie persistante : je travaille sur les applications de la topologie algébrique à l’analyse musicale. L’objectif est de mieux comprendre la richesse de certaines structures musicales à l’aide de ces outils topologiques.
Pourquoi avez-vous choisi ce sujet ?
J’ai toujours adoré les mathématiques, mais je suis avant tout passionnée de musique ! Au cours de mes études, j’ai eu l’opportunité de combiner ces deux domaines, et j’ai la chance à présent de passer beaucoup de mon temps de travail à faire des mathématiques, tout en les appliquant à mes musiques préférées.
Comment cette thèse s’insère-t-elle dans vos projets ?
Je souhaite depuis toujours enseigner les mathématiques ; le doctorat m’a ouvert énormément de portes dans cette voie : j’ai pu explorer le monde de la recherche, découvrir celui de l’enseignement (je suis par ailleurs agrégée de mathématiques), mais aussi celui de la médiation scientifique, grâce à mon domaine de recherche interdisciplinaire. Cette thèse a conforté mon envie profonde d’enseigner, mais m’a également montré qu’il existait un vaste monde à explorer entre les mathématiques et la musique, et j’ai découvert à quel point il est enrichissant de le partager avec un large public !
Enfin, je suis membre de l’association Femmes et mathématiques, ce qui me permet de m’investir dans des actions de médiation visant à promouvoir la place des femmes dans les filières scientifiques.
De nombreux phénomènes musicaux présentent une périodicité, tels que l’équivalence des octaves ou encore la périodicité rythmique. En mathématiques, il existe des outils permettant de modéliser de telles structures : les congruences. Prenons par exemple la mélodie ci-dessous : chaque note musicale qui compose cette mesure peut être caractérisée par sa position et sa hauteur, représentées respectivement par l’axe horizontal et l’axe vertical.
Une première mélodie à modéliser.
La position de la note correspond au moment où celle-ci apparaît dans la mesure, autrement dit le moment où elle est jouée : la première note – le do – apparaît au temps 0, puis on découpe le temps selon une unité bien choisie et on associe un numéro à chacune des notes qui suivent. Le plus souvent, cette unité de temps est choisie selon la plus courte durée, ici la croche, de sorte que la noire compte pour 2, la noire pointée 3, etc. Ainsi, on compte huit temps dans la mesure, ce qui signifie que l’on travaille « modulo 8 ».
De la même façon, on associe à chaque note une hauteur, qui correspond en quelque sorte à la « valeur » de la note jouée (en termes de fréquences). En analyse musicale, on considère souvent les hauteurs modulo une certaine unité appelée l’ambitus (qui désigne l’étendue d’une mélodie, d’une voix ou d’un instrument, entre sa note la plus grave et sa note la plus élevée). En particulier, on se concentre ici sur le nombre d’octaves utilisées pour composer la mélodie : si les notes vivent toutes dans une octave (douze notes), alors on travaillera « modulo 12 », avec la convention que le do vaut 0. On travaille ici en enharmonie, c’est-à-dire que l’on identifie un do dièse avec un ré bémol, un ré dièse avec un mi bémol…
Modéliser des évènements musicaux
Une mélodie est ainsi décrite par la position des notes dans la mesure et leur hauteur, modulo le nombre d’unités de temps dans une mesure et le nombre de notes dans l’ensemble des octaves utilisées. En mathématiques, ces informations sont modélisées en considérant les positions et les hauteurs des notes d’une mesure comme des sous-ensembles d’un ensemble « plus gros », à savoir l’ensemble ℤ/nℤ des entiers modulo n. Sur notre exemple, on prend n = 12 pour signifier que l’on travaille dans une octave, et n = 8 pour signifier que l’unité de temps choisie est la croche. On obtient ainsi deux structures P et H (positions et hauteurs), que l’on peut ensuite combiner de façon à obtenir une description périodique (P, H) de la mesure en termes de position et de hauteur des notes.
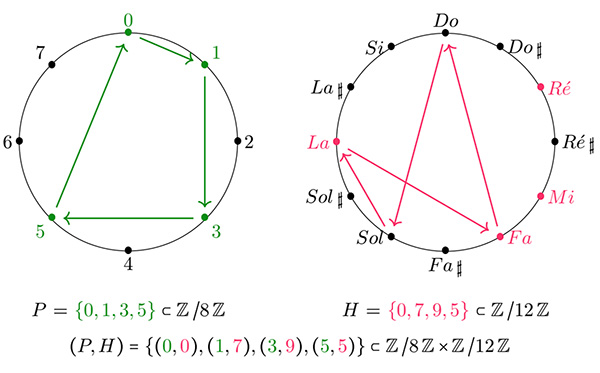
La mélodie précédente sous forme de polygones et de structures périodiques.
La modélisation des mesures donne la possibilité de convertir un morceau en un nuage de points, c’est-à-dire un ensemble de points que l’on peut comparer à l’aide d’une distance. Considérons une partition, issue d’un morceau de musique. Celle-ci est découpée naturellement via des « mesures », chacune étant décrite dans (ℤ/tℤ)×(ℤ/hℤ), avec t une unité de temps et h la hauteur avec laquelle on souhaite travailler (c’est-à-dire le nombre d’octaves multiplié par 12). Chaque mesure est donc réduite à un seul point (P, H) du nuage de points final. Pour les comparer, on utilise ici la transformée de Fourier discrète. Cette dernière a été introduite par le compositeur et théoricien de la musique David Lewin (1933‒2003), dans le but de caractériser des structures musicales en utilisant, entre autres, leur périodicité, mesurée à l’aide de coefficients de Fourier. Ce sont ces mêmes coefficients que nous utiliserons pour calculer la distance entre les mesures d’un morceau de musique.
Si (P, H) est une mesure modulo t et h et (x, y) une note dans cette mesure (avec x sa position et y sa hauteur), alors le coefficient de Fourier associé est donné par la formule suivante :
Pour chaque note on obtient un coefficient et, pour toute une mesure, une matrice (un tableau) de coefficients. Ainsi, chaque partition est découpée en mesures auxquelles on associe des matrices de coefficients de Fourier, puis on calcule la distance entre les mesures en calculant la distance entre les matrices associées, ce qui se fait naturellement à l’aide d’une norme bien choisie. C’est ainsi que l’on obtient bien un nuage de points à partir d’une partition.
De la topologie sur des partitions
À l’aide de la modélisation précédente, on va pouvoir convertir la musique en formes géométriques, plus particulièrement topologiques : les filtrations de graphes. Un graphe est un assemblage de sommets et d’arêtes, et une filtration est simplement une suite croissante de tels objets. Si l’on se donne une partition, alors chaque sommet en représente une mesure et, pour chaque couple de mesure, une distance est associée via la transformée de Fourier. On classe ensuite les distances par ordre croissant, et on ajoute successivement les arêtes correspondant à chaque distance (et donc à chaque couple de mesures). On peut également complexifier la filtration, en remplissant certains triangles, certains tétraèdres… selon une règle fixée, ce qui permet d’ajouter par exemple des informations musicales. Les graphes ainsi obtenus sont alors appelés des complexes simpliciaux. Le nuage de points construit précédemment est donné à la première étape de la filtration, et celle-ci contient donc autant d’étapes que de distances différentes !

Une filtration de graphes associée à une partition.
La question qui se pose à présent est la suivante : comment analyser de tels objets ? On utilisera pour cela des outils topologiques (la topologie est une branche des mathématiques qui étudie les objets de la vie quotidienne « à déformation près » : si l’on imagine une tasse faite en pâte à modeler, on peut s’arranger pour la transformer en un donut, ce que l’on ne pourra jamais obtenir avec un ballon de basket, qui aura au contraire toujours la forme d’une balle). En topologie, et plus particulièrement en topologie algébrique, un travail important consiste à classifier les objets en leur associant des signatures topologiques ; l’homologie en fait partie. Cette dernière compte le « nombre de trous » ou « boucles » dans toutes les dimensions d’un même objet : par exemple, un triangle vide possède un trou en dimension 1, et une sphère (toujours vide) en possède un en dimension 2.
Dans notre cas, l’objectif est de mesurer ce type d’information dans une filtration de graphes : autrement dit, on étudie l’évolution des boucles qui sont formées au cours de la filtration. Ce sont précisément ces informations qui constituent notre signature topologique. On appelle cela l’homologie persistante, car on s’intéresse aux caractéristiques topologiques qui « persistent » au cours de la filtration.
L’évolution de l’homologie dans une filtration peut facilement être représentée visuellement à l’aide de graphiques que l’on appelle des codes-barres : si une boucle apparait à un moment t de la filtration, par exemple avec un triangle, et que cette boucle disparait au temps t + n (par exemple si le triangle est rempli), alors on trace une barre de longueur n dont les extrémités sont données par les points d’abscisses t et t + n, respectivement. Autrement dit, chaque barre mesure exactement la durée de vie des boucles au cours de la filtration, avec en abscisses le moment où ces boucles apparaissent et disparaissent. En clair, ce sont ces graphiques qui mesurent les informations topologiques que l’on souhaite étudier sur notre filtration.
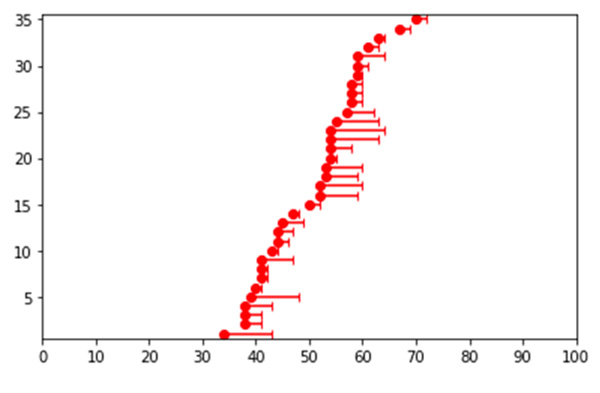
Un exemple de code-barres.
L’homologie persistante et les codes-barres sont des outils puissants en analyse topologique de données, c’est-à-dire lorsque l’on souhaite caractériser plusieurs objets de départ par une signature topologique pour les analyser et les comparer. Par exemple, elle peut servir en astronomie pour classifier des constellations, ou encore en médecine pour comparer des assemblages de neurones.
Ici, on propose de l’utiliser dans un contexte un peu différent, celui de l’analyse musicale ! Comment faire en pratique ? Le point de départ de la thèse a été de comprendre comment associer une filtration de complexes simpliciaux à une partition de musique.
Une fois ce procédé effectué, le but est alors d’étudier les codes-barres associés : cela va permettre d’analyser les partitions, plus particulièrement de les comparer.
En fonction du style musical
Un problème très courant dans le domaine des mathématiques appliquées à l’analyse musicale est celui de la classification automatique du style (créer un algorithme qui prend en entrée une partition, sous la forme d’un fichier MIDI ‒ pour musical instrument digital interface ‒, et qui renvoie le genre musical ‒ pop, rock, jazz…‒). Si la thèse n’a pas encore permis d’obtenir de résultats systématiques, elle offre des pistes prometteuses dans cette direction : en comparant les codes-barres obtenus pour plusieurs morceaux donnés, nous avons pu regrouper des artistes et compositeurs selon le style des partitions étudiées. Une illustration du type de résultat ainsi obtenu est donnée par la figure suivante : on y trouve différents clusters (ensembles) obtenus en comparant le compositeur Jean-Sébastien Bach (1685‒1750) à différents groupes et artistes des genres heavy metal, hard rock, pop et pop rock. Pour Bach, nous avons étudié quarante-cinq morceaux au total, classés en trois styles : quinze sont des préludes, quinze autres des fugues et les quinze derniers sont des chorals. Pour chaque artiste, nous avons sélectionné quinze morceaux de leur discographie. Dans les graphiques, chaque couleur représente un artiste et chaque point correspond à une partition de laquelle a été extrait un code-barres. La légende représente des statistiques qui ont été calculées directement sur les codes-barres afin de les comparer, à savoir la moyenne des longueurs des barres, l’écart type et l’entropie. Cette étudie constitue un premier pas vers la classification automatique du style musical !
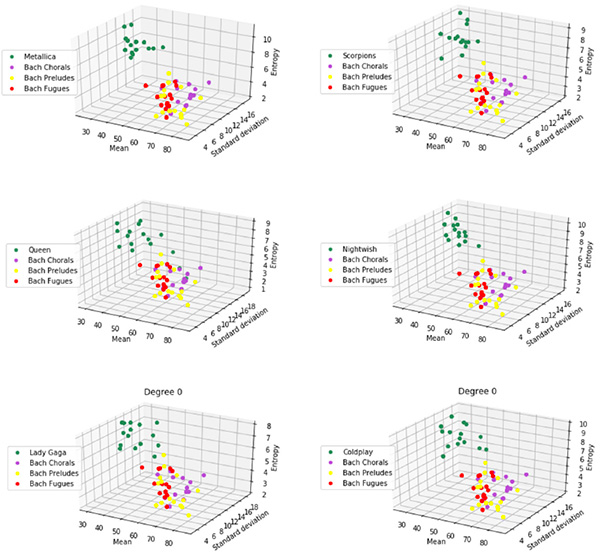
Classification entre Jean-Sébastien Bach et différents groupes/artistes actifs
au cours des cinquante dernières années.
Vers une grande base de données
Il existe beaucoup de méthodes basées sur les mathématiques permettant de mieux comprendre la musique, et les résultats proposés ici n’en sont qu’une toute petite démonstration. Dans le domaine de la classification, il y a encore énormément de travail à faire, ne serait-ce que dans le fait d’élargir le procédé à des styles de musique plus variés (par exemple du jazz, du rap…).
Cela implique de disposer de plus de données musicales à exploiter, et l’un des travaux de la thèse a été de démarrer la conception d’une base de données de fichiers MIDI (disponible sur la page https://math-musique.pages.math.unistra.fr), sur laquelle les documents utilisés sont regroupés, permettant ainsi à la communauté de travailler.
D’autres applications de la topologie à la musique ont été traitées dans la thèse, par exemple en lien avec le Tonnetz d’Euler ou encore l’harmonisation de chansons pop. Les mathématiques offrent encore beaucoup d’applications musicales à découvrir et explorer !

.jpg)